Quiconque souhaite adresser le sujet du modelage sonore sur Oric se verra tôt ou tard confronté à un des “défaut” de son générateur de son le AY-3-8912: la non linéarité du convertisseur numérique analogique utilisé dans le circuit d’enveloppe.
Cet article présente un procédé de compensation de cette non linéarité capable de s’adapter à différents volumes sonores. Ce mécanisme de linéarisation, en plus de fournir une commande proportionnelle d’amplitude ouvre la porte à la génération d’enveloppe très précise dont la granularité s’adapte automatiquement au volume sonore choisi.
Position du problème
Avant de nous lancer dans le contournement d’un problème, commençons par en cerner l’essence. Quel est exactement le problème de non linéarité du machin truc ?
Le schéma de principe ci-dessous illustre le fonctionnement de la génération sonore sur un Oric en même temps qu’il introduit les grandeurs dont il va être question dans la suite de l’article.
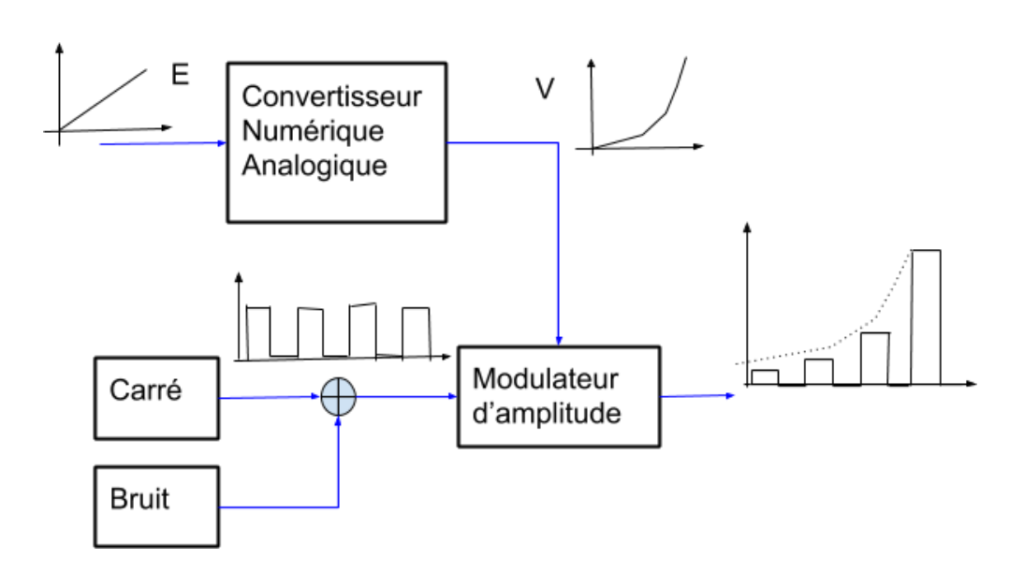
Pour générer un son le PSG AY-3-891x utilise un générateur de signal carré dont il module l’amplitude proportionnellement à une tension issue de la conversion numérique analogique de la valeur d’enveloppe programmée dans le registre d’amplitude. Malheureusement, la conversion numérique vers analogique est entachée d’une non linéarité qui fait que la tension obtenue en sortie n’est pas proportionnelle à la valeur programmée dans le registre d’amplitude. Sur le schéma ci-dessus, on vois que la tension V a une forme arrondie là où la commande d’enveloppe E est en rampe rectiligne.
Ce “problème” est clairement décrit dans les données techniques du composant AY-3-891x, à travers les figures 8 et 9 du document “PSG AY-3-8912 Data Manual” ou entre les figures 2 et 3 du datasheet du PSG AY 3 8912 reproduites ci-dessous:
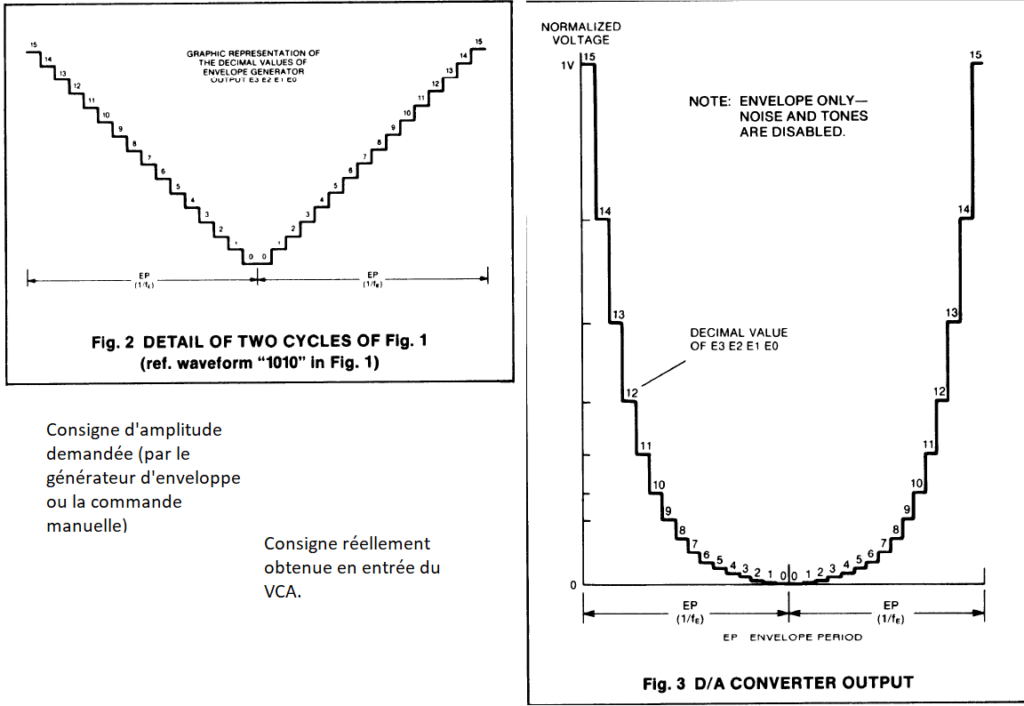
La figure ci-dessous montre clairement que, là où le générateur d’enveloppe ou la commande manuelle de l’amplitude demande un signal triangulaire (à gauche), la commande analogique en entrée du VCA (Voltage Controlled Amplifier) se trouve être d’aspect plutôt franchement parabolique (figure de droite). Et ce phénomène est pleinement assumée avec l’explication suivante:
Since the primary use of the PSG is to produce sound for the highly imperfect amplitude detection mechanism of the human ear, the D/A conversion is performed in logarithmic steps with a normalized voltage range from 0 to 1 Volt.
datasheet AY-3-8912
Ce qui peut se traduire par:
Puisque la fonction première du PSG est de produire un son à destination du mécanisme hautement imprécis qu’est l’oreille humaine, la conversion numérique analogique est effectuée à l’échelle logarithmique avec une plage de tension normalisée entre 0 et 1 volt.
L’oreille humaine est indéniablement moins précise qu’un modem ou un oscilloscope mais elle est capable de faire la différence entre un violon qui joue un La et un piano qui joue un La .. Et la différence repose, en grande partie, sur l’enveloppe sonore dont cette phrase nous suggère qu’elle peut aisément s’accommoder d’une échelle logarithmique en lieux et place d’une échelle linéaire.
Quelqu’un qui souhaite tenter de faire générer un son précis au AY-3-391x sera bien obligé de se poser la question suivante.
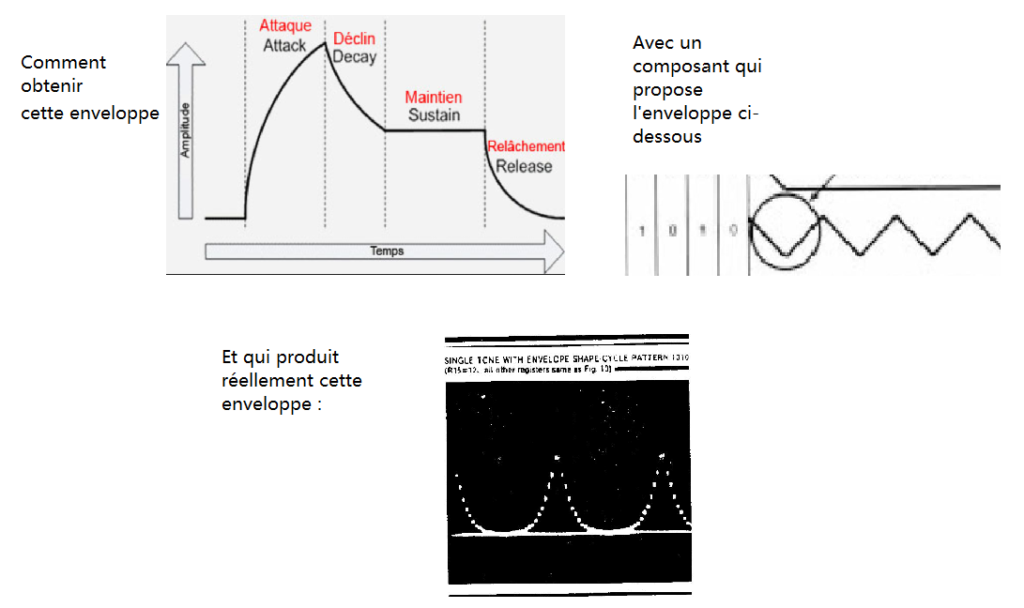
Et dans cet article, je propose une solution qui consiste à linéariser la commande d’enveloppe par une pré-compensation logicielle de la déformation à laquelle on veut échapper.
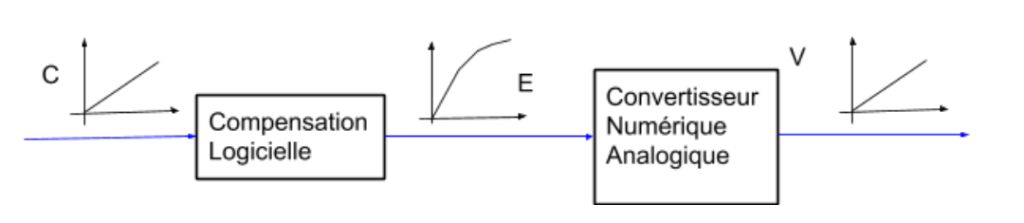
Pour obtenir une tension V qui soit le plus possible proportionnelle à une consigne d’enveloppe C, on peut élaborer une commande d’enveloppe E qui opère une déformation inverse à celle que va produire la conversion numérique analogique.
Techniquement, cela consiste à appliquer une transformation à la donnée que nous voulons programmer dans le registre d’amplitude du AY-3-391x. Une transformation qui tente de compenser et d’anticiper les dégâts occasionnés lors de la conversion en analogique de notre souhait d’amplitude formulé numériquement.
Identification de la déformation
Dans la version General Instrument du datasheet du AY-3-391x, on trouve une version quotée de la déformation qui nous intéresse.
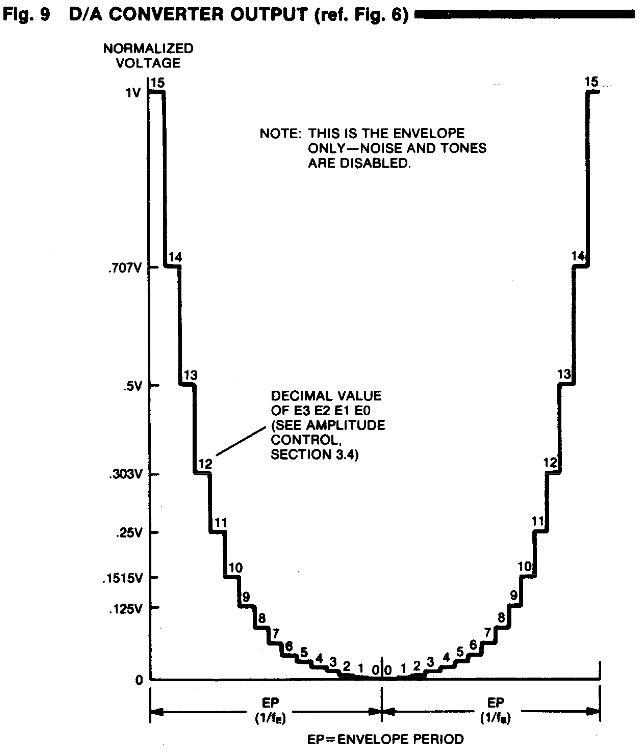
Des quelques valeurs fournies sur ce graphique, on peut déterminer une tendance :
- La valeur de 0.707V pour 14 correspond à 1/sqrt(2)
- La valeur de 0.5 V pour 13 correspond à 1/sqrt(4)
- La valeur de 0.25 V pour 11 correspond à 1/sqrt(16)
Il vient assez naturellement que la tension V en sortie de convertisseur est exprimable par la formule suivante :
V = 1 / SQRT(2(15-E))
où :
Eest le contenu du registre de contrôle de l’amplitude (valeur entière entre 0 et 15).Vest la tension (valeur réelle entre 0 et 1 V)
Dans google, on peut vérifier que la courbe obtenue est proche de celle du modèle.
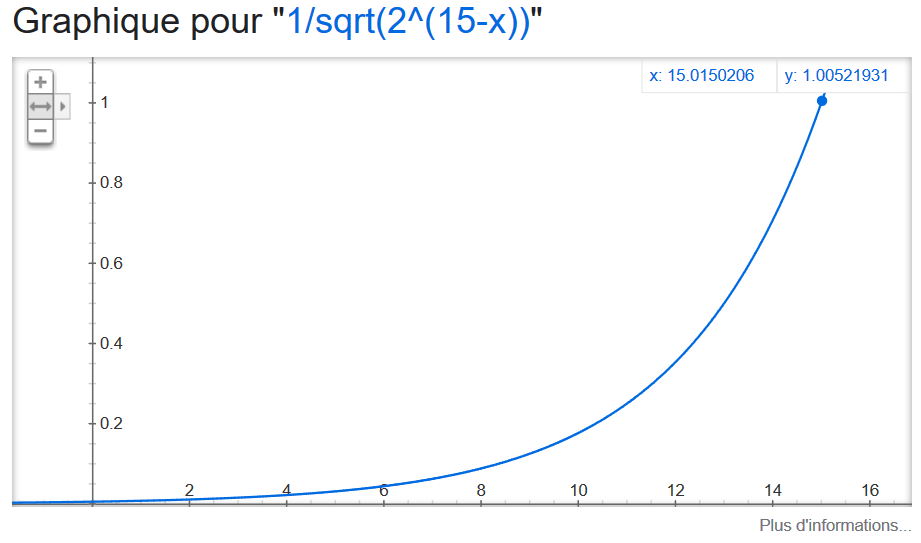
Compensation de la déformation
Pour inverser cette fonction (et donc compenser son effet) on devra calculer la commande d’enveloppe E par la formule suivante:
E = 15-LOG2(1/(V2))
où :
Vest la tension (en volt) que nous voulons en sortie du convertisseur N/AEest la commande d’enveloppe que nous devons programmer dans le PSG pour obtenir la tensionV.
La forme de cette fonction nous donne bien à penser qu’elle compensera la courbe précédente.
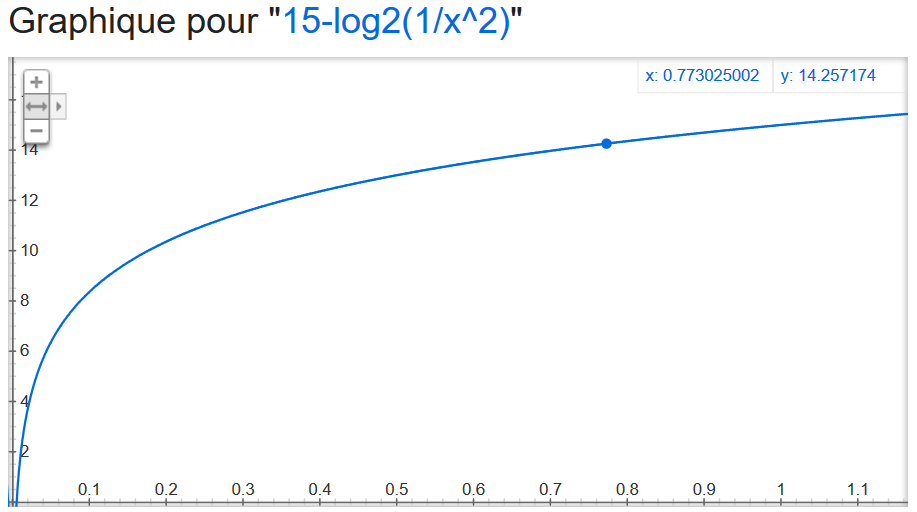
Maintenant que nous avons une fonction permettant de compenser la non linéarité sur l’ensemble des valeurs possibles en sortie du convertisseur, nous allons voir comment il est possible d’adapter cette compensation à des situations où nous déciderions de limiter le volume maximum sur un canal tout en gardant la même dynamique du domaine d’entrée. Nous renoncerions aux valeurs hautes de la tension (car c’est là que les imprécisions sont les plus grandes) mais nous garderions toujours 16 valeurs possibles de consigne d’enveloppe. L’objectif est double:
- gagner en précision absolue,
- offrir la même expressivité d’un son quelque soit le volume sonore auquel on le restitue.
Adaptation de la compensation en fonction du volume
L’idée clé ici est d’associer à la consigne d’enveloppe maximale (15) un extremum de tension correspondent à un palier réel du composant physique. Ceci afin d’adapter au maximum la dynamique d’entrée au potentiel de sorti et bénéficier au maximum du surcroît de précision que nous offre le sacrifice des niveaux électriques élevés
Nous avons vu au tout début que les paliers de tension du composant physique sont sous la forme: 1/sqrt(2^(15-E))
En injectant cette expression dans l’équation vu précédemment, et en simplifiant, il apparaît que la commande d’enveloppe E à programmer dans le PSG s’exprime par:
E = Volume + 2*LOG2(C)
où :
Volumeest une valeur entière entre 0 et 15,Cest la consigne d’enveloppe exprimée en 15ème du niveau électrique correspondant àVolumeEest la commande d’enveloppe que nous devons programmer dans le PSG pour obtenir la tensionV = C*(15/Volume).
Cette expression est d’une telle simplicité qu’elle m’a très fortement fait douter de mes calculs. J’ai donc écris un petit script python pour:
- modéliser la déformation engendrée par le convertisseur numérique analogique,
- calculer une table de compensation pour chaque volume sonore (de 0 à 15),
- simuler l’effet de la pré-compensation,
- comparer avec le cas sans compensation.
Voilà les résultats obtenus pour le volume maximal de 15.
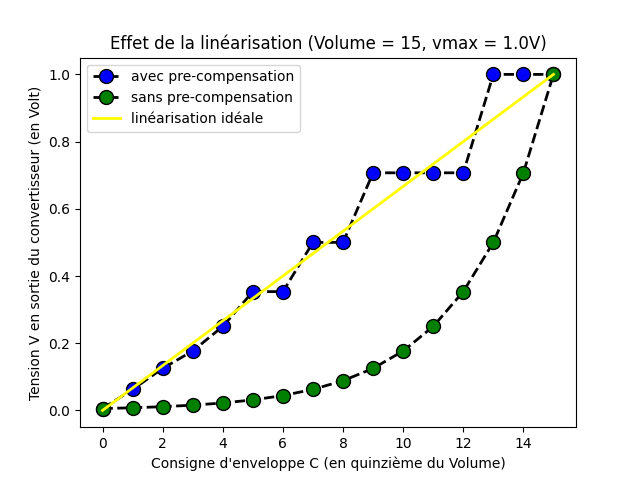
Les points verts représentent la tension électrique obtenue lorsque le registre d’amplitude du circuit d’enveloppe n’est pas transformé. La valeur programmée est directement celle de l’axe des abscisses.
La ligne en jaune représente la tension électrique idéale qui serait obtenue si la conversion numérique analogique était purement linéaire et que nous disposions d’un nombre infini de bit pour exprimer la consigne.
Enfin, les point bleus représentent la tension électrique obtenue par la transformation de la consigne à travers une table de compensation générée par les équations fournies plus haut.
Nous constatons que les points bleus et vert reposent bien tous sur les mêmes paliers réels du composant physique mais qu’ils sont arrangés de telle sorte que leur éloignement à la courbe idéal soit le minimum possible.
L’effet de la linéarisation est indéniable. Voyons comment se comporte l’adaptation de la compensation pour le cas de volume maximum que nous fixerions à certains paliers du composant (paliers pour E=14 et E=12).
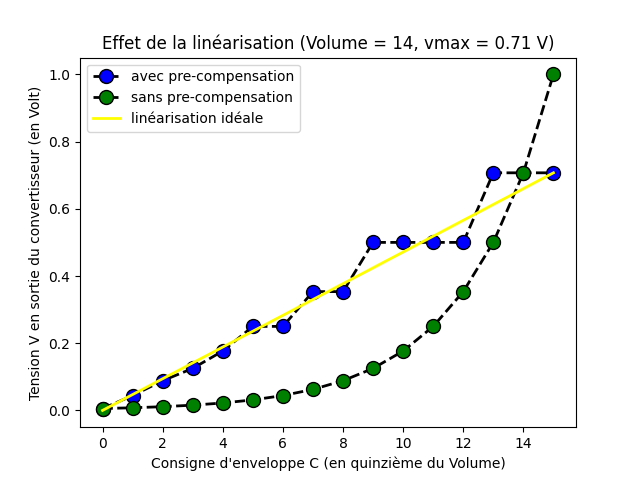
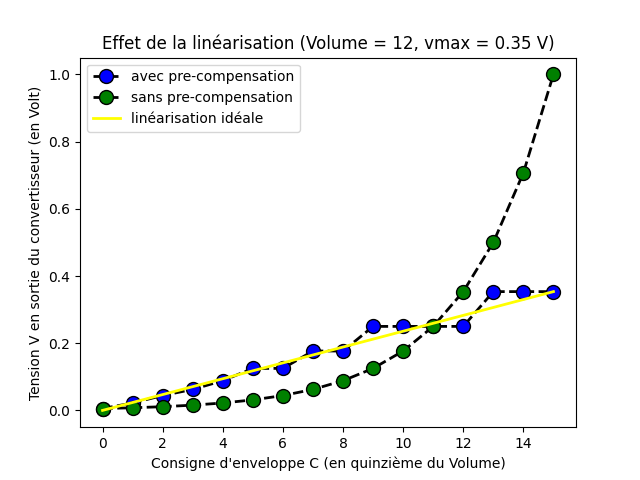
L’adaptation de la compensation semble effective.
Cette étude théorique a permis de:
- démontrer la faisabilité mathématique d’une linéarisation acceptable du comportement du circuit d’enveloppe du PSG AY-3-391x,
- exposer le matériel algorithmique nécessaire à mise en œuvre d’une compensation adaptative.
Vous pouvez télécharger ci-dessous le script python qui m’a servi à générer la table de compensation, simuler son utilisation et vérifier les résultats.
Ce genre de table est le principe utilisé pour rejouer des échantillons 8 bit en utilisant les trois canaux du AY pour donner des valeurs plus proches de la valeur d’origine.
Je l’ignorais mais cela ne me surprend pas car c’est incontournable pour obtenir un peu de précision.
Sais-tu si ce genre de table est utilisé dans une phase de prétraitement des échantillons (les échantillons intègre cette compensation pour éviter d’avoir à l’appliquer en temps réel) ou si la compensation se fait au moment du rejeu de l’échantillon ?
J’ai trouvé un moyen simple et rapide d’utiliser ces tables dans un handler d’IT à 50Hz mais je me dis que si les échantillons intègrent déjà la compensation, ça fait toujours économiser des cycles.
Ca ne peut pas etre fait en avance, sinon ca double la taille des échantillons. En gros on utilise trois tables de 256 octets contenant les valeurs entre 0 et 15, donc au total on obtient 12 bits de précision sur les trois registres, qui donnent au final une approximation pas trop mauvaise d’un son 8 bit.
Le seul cas ou on fait ca directement dans le sample, c’est quand on utilise des samples 4 bits, communément utilisés pour faire des “digi drums”.
La démo “Rambo” du Tivoli Pirat, utilise des samples 2 bit et une table de conversion pour convertir en 4 bit non logarithmique, et le son est vraiment très bon.
Se pourrait-il que cette démo Rambo utilise de la modulation Delta?
L’idée d’une telle méthode c’est de stocker la différence entre deux échantillons plutôt que les échantillons.
L’avantage c’est qu’avec peu de bit par échantillon, on peut obtenir un bon résultats.
Les inconvénients sont qu’il faut faire une somme à chaque échantillon (ça prend de la cpu) et qu’on perd de la dynamique ( les grosses variations rapides du signal sont atténuées).
Je suis désolé, JiBe, mais ça me passe largement au dessus de la tête…
Sinon, l’article me semble bien.
Cordialement
André
L’étude de la non linearité de l enveloppe générée par le processeur sonore et de sa compensation est interessante car elle permettrait de paufiner les phonèmes créés pour la synthese vocale, le décortiquage du AY3 8912 nous fera economiser de précieux octets pour éviter de gros “samples” hachés menu des jeux d’époque que l’on a du mal a comprendre et qui sont gourmands en mémoire.